Алгебра_7 класс_системы уравнений_5 урок
Решение задач составлением систем уравнений с двумя переменными.Закрепим умения составлять и решать системы уравнений по условию задачи.
1. Повторим изученный материал.
Сегодня мы с вами продолжим работу по составлению математической модели по тексту задачи. Вы уже знаете, что математическая модель представляет собой уравнение или систему линейных уравнений. Нам с вами известны различные методы решения систем линейных уравнений. Ответим устно на вопросы:
- Что называется системой линейных уравнений?
- Что называют решением системы?
- Что значит решить систему уравнений?
- Сформулируй алгоритм решения системы уравнений графически.
- Сформулируй алгоритм решения системы методом подстановки.
- Сформулируй алгоритм решения системы уравнений методом алгебраического сложения.
2. Решеним задачи составлением систем уравнений с двумя переменными.
Мы повторили методы решения систем линейных уравнений. Они пригодятся нам при решении задач на сегодняшний урок.
№1174
Мать старше дочери на 24 года, а дочь младше матери втрое. Сколько лет матери и сколько лет дочери.
Решение:
Пусть матери х лет, тогда дочери - у лет. Согласно условию задачи составим систему уравнений:
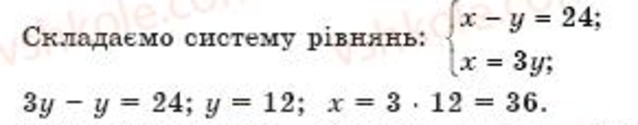
Значит, матери 36 лет, а дочери 12 лет.
Ответ: 36 лет, 12 лет.
№ 1176
В двух седьмых классах - 72 ученика. Если бы из 7-А класса 2 ученика перешли в 7-Б, то в обоих классах учеников стало бы поровну. Сколько учеников в каждом классе?
Решение: Пусть в 7-А классе х учеников, тогда в 7-Б классе у учеников. Согласно условию задачи составим систему уравнений:
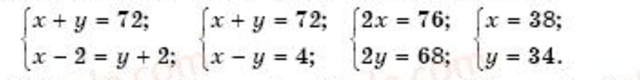
Значит, в 7-А классе 38 учеников, в 7-Б 34 ученика.
3. Домашнее задание.
§ 29 повторить, №1173, №1175.