Алгебра_7 класс_системы уравнений_4 урок
Решение задач составлением систем уравнений с двумя переменными.Тема №4: Решение задач составлением систем уравнений с двумя переменными.
- Научимся составлять системы уравнений по условию задачи;
- Научимся решать задачи с помощью систем двух линейных уравнений с двумя переменными.
1. Ответим устно на вопросы:
Составьте уравнение, зная что:
1) длина прямоугольника х м, ширина у м, а периметр 24 м;
2) основание равнобедренного треугольника a см, боковая сторона b см, периметр 44 см;
3) туристы 5 ч ехали на автобусе со скоростью х км/ч и шли пешком 3 ч со скоростью у км/ч. Весь путь составил 315 км.
2. Изучим новый материал.
Уравнение – это один из типов математической модели. Какие модели мы еще изучали? (системы двух линейных уравнений с двумя переменными).
Где же применяются системы уравнений?
Сегодня мы начнем рассматривать задачи, решить которые можно с помощью систем уравнений с двумя переменными.
Этапы решения задач:
1. Составление математической модели (система уравнений).
2. Работа с составленной моделью.
3. Ответ на вопрос задачи.
Пример.
Схема решения задач:
1) Анализ условия.
2) Выделения двух ситуаций.
3) Введение неизвестных (х и у).
4) Установление зависимости между данными задачи и неизвестными.
5) Составление уравнений.
6) Решение системы уравнений с двумя переменными.
7) Запись ответа.
3. Рассмотрим и решим такие задачи.
№ 1160. Купили 9 м ткани двух сортов ценой по 40 грн. и 30 грн. за 1 м. За всю покупку заплатили 330 грн. Сколько купили метров ткани каждого сорта?
Решение:
Пусть купили х м ткани одного сорта, тогда другого - у м. За ткань одного сорта заплатили 40 х грн, а за ткань другого сорта - 30 у грн.
Всего купили 9 м, тогда х+у=9. Так как заплатили 330 грн., то 40х+30у=330. Составим систему уравнений.
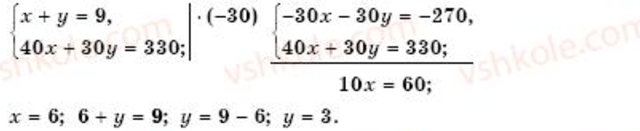
Ответ: 6 м одного сорта ткани, 3 м другого сорта ткани.
№1162.
Скорость моторной лодки по течению - 23 км/ч, а против течения - 17 км/ч. Найдите собственную скорость лодки и скорость течения.
Решение:
Пусть собственная скорость лодки х км/ч, тогда скорость течения - у км/ч. Согласно условию задачи составим систему уравнений:
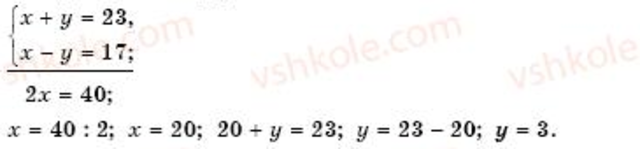
Значит, собственная скорость лодки 20 км/ч, тогда скорость течения - 3 км/ч.
Ответ: 20 км/ч, 3 км/ч.
4. Домашнее задание.
§ 29 прочитать, №1161, №1163 (Учебник для 7 класса "Алгебра" Г.П. Бевз).