Реєстрація
Алгебра 7 класс. Системы линейных уравнений с двумя переменными / Алгебра_7 класс_системы уравнений_1 урок

Алгебра_7 класс_системы уравнений_1 урок

Знакомство с новыми понятиями урока (система уравнений с двумя переменными, решение системы двух линейных уравнений с двумя переменными), графическим способом решения систем линейных уравнений с двумя переменными и количеством решений системы линейных уравнений.

Тема №1: Система уравнений с двумя переменными. Графический способ. 

-   Введём понятие системы линейных уравнений с двумя переменными;

-   Покажем графический способ решения системы линейных уравнений;

-   Закрепим навыки построения графиков линейных функций.

1. Ответим устно на вопросы:

    1.      Какое уравнение называют линейным уравнением с двумя          переменными?

    2.      Что называется решением уравнения с двумя переменными?

    3.      Какой формулой задается линейная функция?

    4.      Что является графиком линейной функции?

    5.      Как построить график линейной функции?

    6.     Является ли линейным уравнение:

                           а) 3y – 2x = 0;                                б) xy = 21;

                           в) –x + 3y = 0;                                г) 0x +y = 6?

     7.    Назовите несколько решений линейного уравнения   0,5x – y = 1.

2. Изучим новый материал.

Система уравнений – это  несколько уравнений, для которых находят общее решение. 

Записывают систему уравнений, объединяя их фигурной скобкой:

 

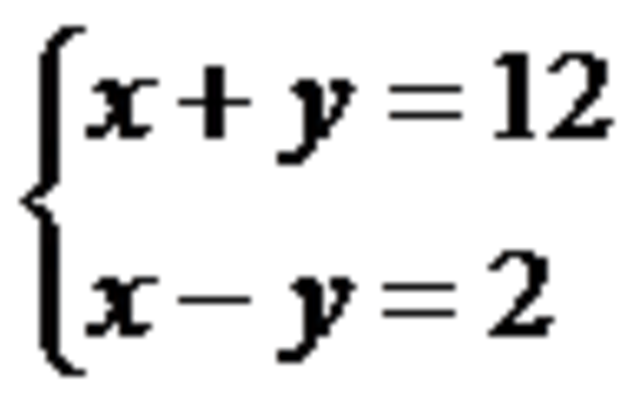
Решение системы уравнений с двумя переменными – это пара значений переменных, обращающая каждое уравнение в верное равенство.

                                    Если х=7, у=5, то   ,        , верно, т.е. (7; 5) – решение системы уравнений.

Решить систему – это значит найти все её решения или доказать, что решений нет.

Решать системы уравнений можно графическим способом.

Алгоритм решения системы уравнений графическим способом:                       
  1. Выразить переменную у в первом уравнении.
  2. Выразить переменную у во втором уравнении.
  3. В одной системе построить графики данных функций.
  4. Координаты точки пересечения графиков и является решением системы уравнений.

Это полезно знать:

Если точек пересечения графиков нет, то система решений не имеет;
 Координаты точек пересечения определяются приблизительно, поэтому и решения могут получиться приблизительными.
Чтобы проверить точность полученных решений, их нужно подставить в уравнения системы!

Пример. Решите графически систему:

            

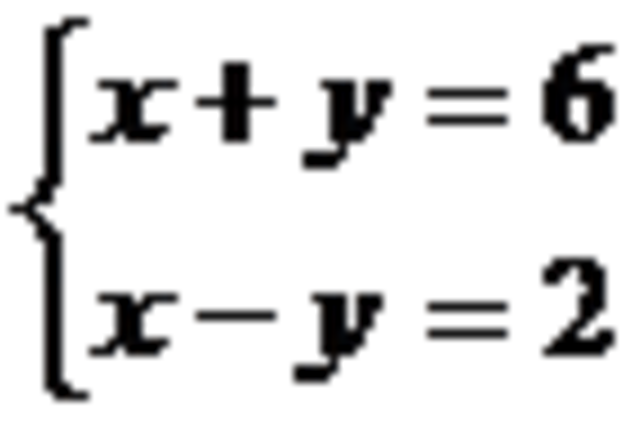
1) х +у = 6   →           у = 6-х   линейная функция, график вида у = kx + b,  k = -1, b = 6

 x 

 0 

 4 

y

6

2

2) х -у = 2   →            x -2 = у

y = x-2   линейная функция, график вида у = kx + b,  k = 1, b = -2

 x 

 0 

 2 

y

-2

0

3) Строим графики функций.

 
   

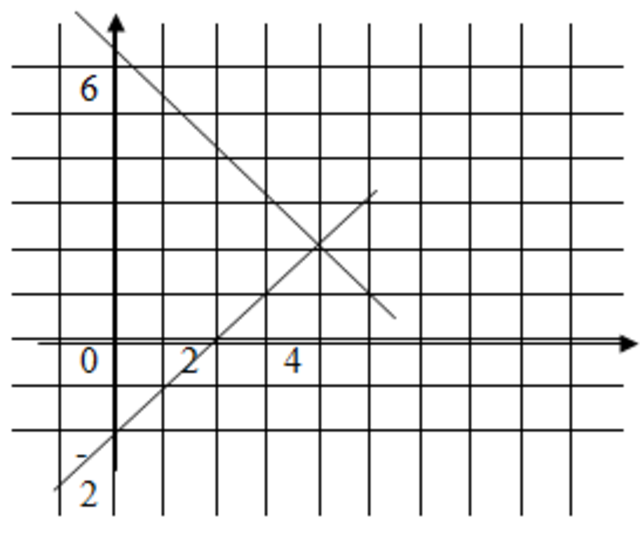
Графики функций пересекаются в точке А(4; 2) Значит, система имеет одно решение (4; 2).

               Ответ: (4; 2)

Сколько решений имеет система уравнений?

                  

 

 1) Если k1=k2, , b1=b2 , то графики совпадают, система имеет бесконечное множество решений.
2) Если k1=k2, b1≠b2 то графики параллельны, система не имеет решений.
3) Если k1≠k2, b1=b2 , то графики пересекаются, система имеет одно решение: (0, b).
4) Если k1≠k2, b1≠b2 , то графики пересекаются, система имеет одно решение (x1, y1). 

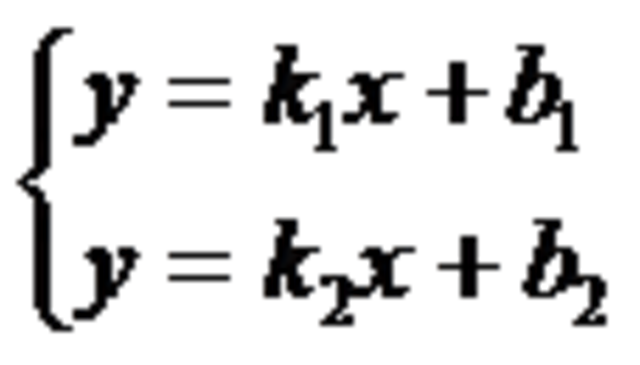
 Примеры:


 

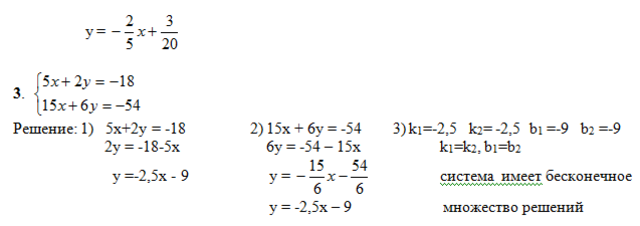
3. Проверим себя:

 - Что называется решением системы уравнений с двумя  переменными?
- С каким способом решения систем уравнений с двумя переменными мы познакомились?
- В чем заключается его суть?
- Дает ли данный способ точные результаты?
- В каком случае система не будет иметь решений?

4. Домашнее задание.

§ 26 прочитать, №1055, №1060, №1062 (Учебник для 7 класса "Алгебра", Г.П. Бевз)