Структури у Всесвіті
Лекція №3 з курсу Людина і космосСтруктури у Всесвіті
Передмова
Для того, щоб зрозуміти суть того чи іншого явища, будову об'єкту, який нас зацікавив, щоб мати змогу створювати щось самому, потрібно мати найбільш загальні уявлення про навколишній світ. Самі по собі допитливість і спостережливість без знань, як і знання без допитливості та спостережливості, мало чого варті. Розум людини побудований так, що він реагує лише на незнайоме, несподіване, на те, що може якось вплинути на саму людину. Та якщо незвичайне повторюється багато разів підряд, ніяк не впливаючи на життя людини, вона перестає реагувати на нього, а згодом, і помічати. Коли у людини не розвинена розумова та духовна діяльність, в своїх потребах вона реагує лише на сигнали забезпечення життєздатності власного організму, не відрізняючись від рослин і тварин, від всього живого на Землі. Майже вся діяльність такої людини зводиться до того, щоб здобути їжу та одяг, продовжити рід. Та людина стає Людиною з великої літери тільки тоді, коли вона може обійняти своїм розумом Всесвіт, а серцем зрозуміти його, коли вона, навчаючись, стає Творцем, Творцем Прекрасного, Розумного, Гармонійного, Духовного, Творцем Добра. Коли вона живе за законами Всесвіту і в згоді з ними, коли вона не руйнує Природу, а допомагає їй і доповнює її. Та все це можливе лише в тому разі, коли людина має уявлення про основні закони та принципи будови хоча б тієї частки Всесвіту, який обіймає її. Частиною таких уявлень є структури, які мають місце навколо нас. Озирніться, придивіться до того, що вас оточує, і ви зрозумієте, що найпростіші речі та явища, до яких ви звикли - незвичайні, незрозумілі. Що таке час? Що таке простір? Що таке світло? Що таке думка, рух, розум? Безліч таких запитань виникне перед вами. Та не поспішайте з відповідями. Зробіть перший крок за обрій, запитайте про що-небудь у Природи і починайте шукати відповідь. І, можливо, що вам у пригоді стануть і деякі спостереження та уявлення про навколишній Світ, а саме ті, про які піде мова нижче.
Загальні уявлення про космічні структури
Коли ми спостерігаємо за навколишнім світом, то помічаємо, що деякі риси повторюються то тут, то там. Всі рослини різні і всі подібні; крона та коренева система дерев, річкові системи та системи кровообігу — все це таке різне і чимось подібне. Циклони і галактики, вихрові утворення — теж мають щось спільне. Цим спільним є подібність в структурі, в архітектурі їх будови. При цьому змінюються розміри, забарвлення, напрямок, багато інших параметрів, але щось залишається незмінним. Найкращим висловом цієї спільності є вираз: "Куди не подивись — скрізь одне і те ж ". Спільна риса, яка не змінюється й об'єднує структури одного об'єкту, явища чи структури різних об'єктів, називається самоподібністю або інваріантом.
Таких рис в системі, що розглядається, може бути одна, а може — декілька. Одна з них, чи не найпоширеніша, яка характеризує процес чи фігуру, що утворюється завдяки безкінечному повторенню вихідного стану, називається фракталом. В перекладі з англійської мови — це дрібний, розбитий, зламаний. По своїй суті фрактали — це те, що повторюється. Як приклад розглянемо будову сніжинки Коха. Побудуємо рівносторонній трикутник (мал. 1).
 мал.1
мал.1
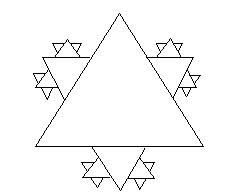
Кожну його сторону розіб'ємо на три частини і на середній побудуємо по рівносторонньому трикутнику. Повторюючи процедуру до нескінченості, ми отримаємо фігуру, яка матиме все більший периметр з обмеженою площею. По суті це і не лінія, і не фігура. Це щось інше. Візьміть квадрат, розбийте його на 9 рівних частин (мал. 2) і виріжте середній квадрат. Інші 8 тим же способом розбийте знову на 9 рівних частин і виріжте знову їх середини, і так до нескінченості. Врешті-решт ви отримаєте конструкцію, яка називається килимом Серпинського, і яка має периметр, що прагне до нескінченості, в той час як площа взагалі наближається до 0.
| |
Для того, щоб описувати такі об'єкти, американський математик Мандельброт ввів для них дрібні системи координат. Візьмемо відрізок прямої. Розділимо його на N рівних частин довжиною R=1/N, звідки N=1/R. Якщо взяти квадрат і розділити його теж на N рівних частин, то N=1/R2. Для куба— N=1/N3. В загальному випадку R=1/Nn, де n— число координат фігури.
З останньої формули знайдемо, що
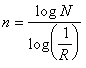
Для сніжинки Коха ми брали сторону трикутника і розбивали на N1 = 3 частин, потім обумовлювали процедуру, згідно з якою пряма перетворювалась в ламану, тобто а) ![]() б)
б) ![]()
![]()
Довжина виміру у нас R=1/N=1/3. Розмірність лінії б) становить
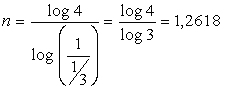
Ця розмірність близька до розмірності берегової лінії, для якої n=1,15...1,25. Для килима Серпинського, в якого N=8 (дев'ятий квадрат ми відрізали), розмірність n=1,89. Як бачимо, розмірність фракталу залежить від характеру його будови, бо з одного боку він показує ступінь заповнення простору даною конструкцією, з другого—її ламаність.
В залежності від того, що є інваріантом процесу чи будови, змінюється і вигляд фракталу. Наприклад, для дерева, як інваріанта, можна використати площу перетину стовбура. Щоб вона залишалась незмінною, потрібно, щоб площа перетину гілок першого, другого і т.д. поколінь дорівнювала площі перетину стовбура, а саме:
![]()
Від площі перетину гілок залежить міцність дерева, і якщо S зберігається для всіх поколінь гілок, то дерево має скрізь однакову міцність. Зовсім інша справа для системи кровообігу чи системи водозабезпечення міста. Інваріантом таких систем буде вже інший параметр. Який саме? Поміркуйте і надішліть на це відповідь.
Щоб у вас не склалось враження, що фрактали мають лише геометричний характер, приведемо декілька прикладів іншої природи. Маса галактик, зоряних скупчень, сузір'їв, планетних систем підкоряються закономірності зміни маси; дитячі садки, школи, вищі навчальні заклади, аспірантура—це інша закономірність (яка?) і т.д. Фрактали мають місце в музиці і в поезії, в кількості і розмірі озер і масляних плям на воді, при конденсації пару і в хімічних процесах.
Характерними особливостями фрактальних структур є: а) кінцевий вигляд фрактала не залежить від вихідної фігури і визначається алгоритмом перетворення. Наприклад, якщо в коло ми впишемо три кола, а в кожне з них ще по три і т.д., то вже через кілька таких повторень ми побачимо, що межа окреслює рівносторонній трикутник(мал.3).
Другим, дуже цікавим і надзвичайно важливим прикладом в Природі є схема трикутника Паскаля для вивчення біноміальних коефіцієнтів (мал. 4).
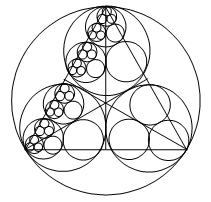
Мал.3
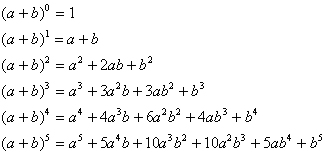
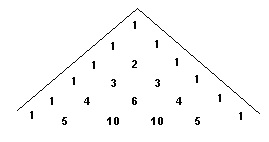
Мал.4
Як бачимо, для знаходження відповідних біноміальних коефіцієнтів необхідно скласти два, що стоять вище в трикутнику. А тепер візьміть систему труб (мал. 5) і через отвір зверху висипте, наприклад, 1 кг цукру. На кожному розгалуженні цукор буде розподілятись порівну між трубками, що йдуть вниз—вліво і вправо. Якщо взяти значення чисельників, то це будуть ті ж самі цифри, що і в трикутнику Пуассона.
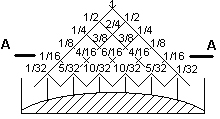
Поставимо внизу під системою трубок одного діаметра ящик з перегородками і побачимо, що засипаний зверху цукор розподілиться по лінії, яку називають кривою Гауса. Так от, якщо замість одного отвору ми будемо сипати той же 1 кг цукру в декілька, наприклад, на рівні А-А , причому в якій завгодно пропорції, то в кінці все одно буде та ж крива Гауса. Головне, щоб алгоритм розгалуження потоку був 1/2, а процедура повторювалась якомога більше разів.
Другою особливістю фрактальних структур є те, що розмірність їх дробова, хоча слід зауважити, що у точки n=0, у лінії без зламів, як і у кола n=1, у плоских фігур без порожнин n=2, в заповнених об`ємних тіл n=3, а от в системі кровообігу n=2,7.
Третьою особливістю фрактальних структур є самоподібність, про яку йшла мова вище. В цій особливості віддзеркалюється надзвичайно важливий принцип будови Всесвіту, згідно з яким найменша частина Всесвіту несе в собі інформацію про будову всього Всесвіту. Як казали філософи давнини, "пізнай себе—пізнаєш світ".
Фрактали мають дуже різноманітну природу, та все ж їх можна розділити на просторові, часові, інформаційні та комбіновані. Серед наведених вище прикладів були розглянуті просторові та просторово-часові. Як приклад часового фракталу можна привести процес радіоактивного розпаду, ланцюгові реакції, перерозподіл енергії в однорідних середовищах та таке інше. Найменш дослідженими і при цьому найбільш цікавими є інформаційні фрактали, а серед них ті, що відповідають за передачу спадковості. Відомо, що інформація про спадковість передається через ДНК — надзвичайно складну структуру, в якій закладена інформація про будову та розвиток живого організму. Та якщо уважно придивитись до навколишнього світу, то принцип накопичення інформації і її використання для побудови самоподібних об`єктів та протікання самоподібних процесів використовується у Всесвіті завжди і скрізь. В момент народження Всесвіту є своє ДНК, свої фрактали, які, можливо, закладені в час згасання іншого Всесвіту, так само , як закладаються ДНК майбутнього при дозріванні рослин.
Принцип фрактальності лежить в основі всіх еволюційних процесів. Гарною ілюстрацією фрактальності життя є гра "життя", яку запропонував Д.Конвел. Якщо всі клітини листа паперу " в клітину" визначити живими при наявності в них крапки і мертвими за її відсутності, а також ввести правила гри, при яких клітина оживає при наявності трьох живих сусідів, не змінює стану при n=2 і лише при n=1, або n![]() 4 гине (всього сусідів у кожної клітини 8:4 по ребрах та 4 по вершинах), то початкова структура починає розвиватись, взаємодіяти з іншими структурами, розмножуватись, здобуває імунітет, захоплює "життєвий простір", захищається. На мал.6 приведено приклади ігрових фракталів Конвела. Фігура 6а називається “планером”, (вона показана в розвитку), фігура 6б — “крокодил”, фігура 6в — “планерна рушниця”.
4 гине (всього сусідів у кожної клітини 8:4 по ребрах та 4 по вершинах), то початкова структура починає розвиватись, взаємодіяти з іншими структурами, розмножуватись, здобуває імунітет, захоплює "життєвий простір", захищається. На мал.6 приведено приклади ігрових фракталів Конвела. Фігура 6а називається “планером”, (вона показана в розвитку), фігура 6б — “крокодил”, фігура 6в — “планерна рушниця”.
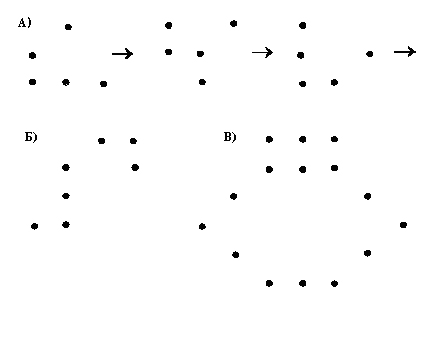
Мал.6
Ще однією важливою особливістю фрактальних структур є заповнюваність простору. Сніжинка Коха прагне до кола; а коло на мал..3 до трикутника. Зовнішній вигляд мінералу, рослин, планетної системи визначається фракталами, які закладено в їх будову. Кордони фрактала розташовуються там, де число народжених клітин дорівнює числу помираючих, де вже немає "життєвого простору", де недосить енергії, або її забагато. Туж картину можна спостерігати і по масі, по зарядах, по інформації та т.п.
Фундаментальну роль у будові Всесвіту відіграють фрактали, пов'язані з трансцендентними числами: фі— золотим перетином, e — основою натуральних логарифмів та пі — числом переходу від прямих ліній до кола, від кубічних форм до сферичних. Золотий перетин фі — це число, яке задовольняє пропорції
![]()
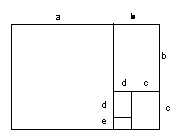 (мал. 7):
(мал. 7):
і яке задає самоподібність прямокутників
![]()
Потрібно відзначити, що число φ надзвичайно поширене в архітектурі, в будові живого і неживого світу.
Не менш важливу роль в будові об'єктів Всесвіту відіграє число π.
Щоб зрозуміти цю роль, необхідно відстежити залежність між площею поверхні та об'ємом кубічних і сферичних фігур в залежності від числа координат простору, а саме для квадрата і кола, для куба і сфери, для n - вимірних кубів та сфер. Для розуміння ролі числа π важливо також те, що просторові фрактали прагнуть або до кубічних форм, або до сферичних в залежності від того розвивається процес чи завершується.
Число е лежить в основі майже всіх процесів, що відбуваються у Всесвіті. Фізичну суть числа е можна зрозуміти на прикладі витікання води з ємкості з отвором біля дна. Швидкість витікання буде залежати від висоти стовпа рідини в ємкості і буде змінюватись по закону, в основі якого знаходиться число е. По такому ж закону протікає розпад радіоактивної речовини, де кількість речовини, що розпалась, залежить від тієї кількості радіоактивної речовини, що залишилась. В основі всіх процесів розпаду, перетворень, перерозподілу речовини і енергії, всіх хвильових процесів лежить число е, часовий фрактал, характерний для всіх змін в часі.
Для розуміння космічних структур обов'язково потрібно зупинитись на теоремі Кюрі, згідно з якою симетрія середовища розповсюджується на будову об'єкта, що в ньому знаходиться, і навпаки: в залежності від симетрії об'єкта перебудовується структура середовища, яка його оточує. Згідно з цією теоремою фрактальність структур відстежуватиметься не лише на одному рівні організації матерії, але й на різних. Так від параметрів Землі, як планети, залежать параметри всіх об'єктів і структур на Землі як неорганічних, так і органічних.
Загальні для різних об'єктів та процесів фрактали об'єднують їх в системи більш високого рівня, визначають їх стійкість. Системи, що мають одну й ту ж , або подібні фрактальності, взаємодіють між собою. Характер взаємодії може бути позитивним, якщо структури доповнюють одна одну і негативним, коли вони взаємно виключають одна одну. На формування різних структур впливають початкові неоднорідності, а саме різного роду потенціали, злами і тріщини, пустоти і непритаманні даному об'єкту чи середовищу включення, тобто все те, що порушує будову і характеристики системи, яка розглядається. Навпаки: регулярні структури будуть формувати нові якості і властивості. В цьому ще багато незрозумілого: які структури, яким чином і в яких умовах формують ті чи інші ефекти. Цікавими в цьому розумінні є досліди В.Гребинникова. Так бджолині соти викликають у піддослідних почуття пружинної перепони, змінюють самопочуття, з'являється металевий присмак, в очах іскри ( аж до галюцинацій), змінюються й інші відчуття: тепла і холоду, тяжіння і невагомості, тощо. Подібні ефекти спостерігаються під впливом багатьох інших регулярних структур, особливо якщо вони знаходяться між людиною і Сонцем, незалежно від положення планети і людини на ній. Від Сонця надходить щось таке, що підсилюється регулярними структурами, або перетворюється в інші фізичні потоки. Сила дії структур на людину з відстанню змінюється не обернено - пропорційно відстані в квадраті, а у відповідності з рядом чисел 4, 13. 20, 40, 80, 120, 150 см і т. д., тобто, підкоряється правилу подібному до правилаТаціуса-Боде для планетарних радіусів Сонячної системи. Та якщо зважити на те, що поверхня Сонця має регулярну структуру, що нагадує сотову, то можна висловити припущення, що сонячні структури формують космічні фрактали, в вузлах яких з одного боку знаходяться планети, з іншого - що вони транслюються на Землю і продовжуються в структурах Землі.
Згідно з теоремою Кюрі подібне взаємодіє з подібним. Взаємодіють не лише сили і процеси, але й регулярні структури подібної фрактальної будови. В. Гребенковим запропонований компас, що реагує не на масу чи заряд, а на структуру. Якщо в скляну банку на павутинці підвісити соломинку, то вона буде реагувати на капілярні структури. Можливо, що в залежності від структури об'єкта, компасом для нього служитиме частка подібної структури. Так лозоходці для пошуку заліза закріплюють на лозу шматок руди або заліза, і чутливість лозоходця значно покращується. Взаємодіють не тільки структури, але й процеси. Так, відомий астроном М. Козирєв виказав припущення, що вулканізм на Землі повинен викликати вулканізм на Місяці, що невдовзі і підтвердив, спостерігаючи виверження вулкану Альфонс. Отже, окрім трансляції структур, транслюються і процеси. Трансляторами фрактальних структур можуть бути не лише космічні тіла, але й всі об'єкти, що є джерелами енергії.
Все, про що сказано вище — це лише невеликий екскурс в незвичайну і ще малознайому країну "космічних структур", країну, яка чекає своїх допитливих дослідників.
Домашнє завдання.
Познайомившись з першими і найбільш загальними уявленнями про космічні структури ви можете вибрати для власного дослідження приклади фрактальних структур, що приведені в тексті, або ті, що оточують вас, ті, що можете знайти в літературі. Ваше завдання описати одну чи декілька структур, визначити їх параметри, та закономірності будови, показати їх місце і значення в природі. Поміркуйте над тим, що визначає їх суть, і, якщо зможете, визначте ту якість, ту властивість, що змінюється при будові структури. Вагомості вашій роботі нададуть власні досліди і власні пояснення.
Як теми для самостійних досліджень можуть бути запропоновані такі:
— дослідження та класифікація геометричних фракталів;
— пошук та дослідження інваріантів просторових, часових та інформаційних фракталів;
— дослідження та класифікація фізичних фракталів;
— дослідження фракталу трикутника Пуасона;
Вказівка: змініть схему розподіл в трикутнику Паскаля з 1/2+ 1/2 на 1/3+2/3; обмежте частину лівої сторони трикутника, виріжте кілька вузлів в середині і подивіться, як зміниться крива розподілу цукру наприкінці. Продумайте інші досліди та зробіть висновки;
— дослідження механізмів формування та передачі спадкової інформації у Всесвіті;
— пошук та дослідження фігур, аналогічних приведеним в грі “життя”;
— дослідження ролі чисел в будові космічних структур.
Вказівка: краще вибрати одне з цих чисел і дослідити його більш глибоко;
— дослідження взаємодії регулярних структур між собою;
— дослідження взаємодії процесів;
— дослідження трансляції структур в просторі і часі;
— дослідження впливу регулярних структур на стан людини, на розвиток і стан рослин, комах та інших живих істот.
Рекомендована література.
1. Успіхи фізичних наук, журнал, Т 146, с 492, 1985
2. Журнал “ Техніка молоді”, №2 за 1979 р., №6 за 1984 р., №10 за 1992 р.
3. Журнал “Свет”, №9-10 за 1993 р.,
4.Фракталы в физике, Мир, М, 1988.
5. Компьютеры и нелинейные явления, М, Наука, 1988.